Composición Corporal parte 2

COMPOSICION CORPORAL, PARTE 2

Por Francis Holway

Introducción:

Hemos ya estudiado el modelo de dos componentes químicos y su implementación con antropometría. Como vimos, existen muchas ecuaciones de regresión predictivas del porcentaje de grasa corporal, y existe mucha variación entre ellas, siendo además muy especificas a la muestra. Recordemos además las tres suposiciones de constancia biológica:

•  densidades de la grasa y masa libre de grasa (mldg) de 0,9 y 1,1 g/ml;
• proporciones fijas de componentes de la mldg;
• densidades fijas de los componentes de la mldg.

Una vez mas, la masa ósea es la que mas afecta la densidad, proporcionando errores de estimación de la densidad de los componentes de la mldg. El diseñador del método, Albert Behnke, y el perfeccionador del mismo, Joseph Brozek, estaban interesados en la cantidad de grasa del cuerpo, ya que estudiaban la solubilidad de gases en la grasa corporal y los estados de obesidad y desnutrición. Para ellos, el modelo cumplía con sus requerimientos de análisis de información. El resto de los investigadores continuaron transitando el camino elegido por esas dos prominencias, aplicando el modelo a una gama diversa de áreas como por ejemplo el deporte.

Es, sin embargo, en el deporte donde la composición corporal se interesa mas por otro componente muy relacionado a la función: la masa muscular. Como escribe Alan Martin (1990), en la mayoría de los deportes de elite los niveles de grasa corporal están en índices mínimos, y la gran variabilidad se debe a diferencias en la masa muscular. Debemos complementar la información de composición corporal con el importante tema de la cuantificación del músculo.

Con fines similares a su aplicación en el deporte y el campo de la salud, el mismísimo Alan Martin (1990) genero ecuaciones para estimar la masa ósea a partir de diámetros medidos antropométrica mente. Una vez mas, simplemente “mejoro” las ecuaciones originales de Matiegka (1921) con coeficientes frescos obtenidos del gran estudio de cadáveres que le sirvió de tesis de doctorado. Trataremos también este tema, pero antes falta ampliar el concepto del pliegue y sus errores.

El pliegue, mitos y realidades

Me he tomado la libertad de copiar el titulo de un clásico de la bibliografía antropométrica publicado por Martin y colegas (1987) que detalla los pormenores de los pliegues. Los autores basan sus conclusiones sobre los resultados del Estudio de Cadáveres de Bruselas (ECB), realizado entre septiembre 1979 y julio 1980 en Bélgica, donde se midieron y diseccionaron 27 cadáveres frescos, siendo los primeros dos utilizados para el estudio piloto. Unos años mas tarde Michael Marfell-Jones y Jan Clarys (1991) realizaron estudios sobre seis cadáveres adicionales, diseccionándolos de manera diferente para generar datos sobre los segmentos corporales con fines mas aplicables a la biomecánica.

Estudio de cadáveres de Bruselas, septiembre 1979 a junio 1980.

El primer estudio sobre cadáveres, publicado en 1984, tenía como objetivos:

• proporcionar datos sobre los tejidos en cadáveres
• estudiar el funcionamiento de las ecuaciones para estimar la composición corporal disponibles hasta la fecha;
• generar nuevas ecuaciones predictivas a partir de los datos nuevos

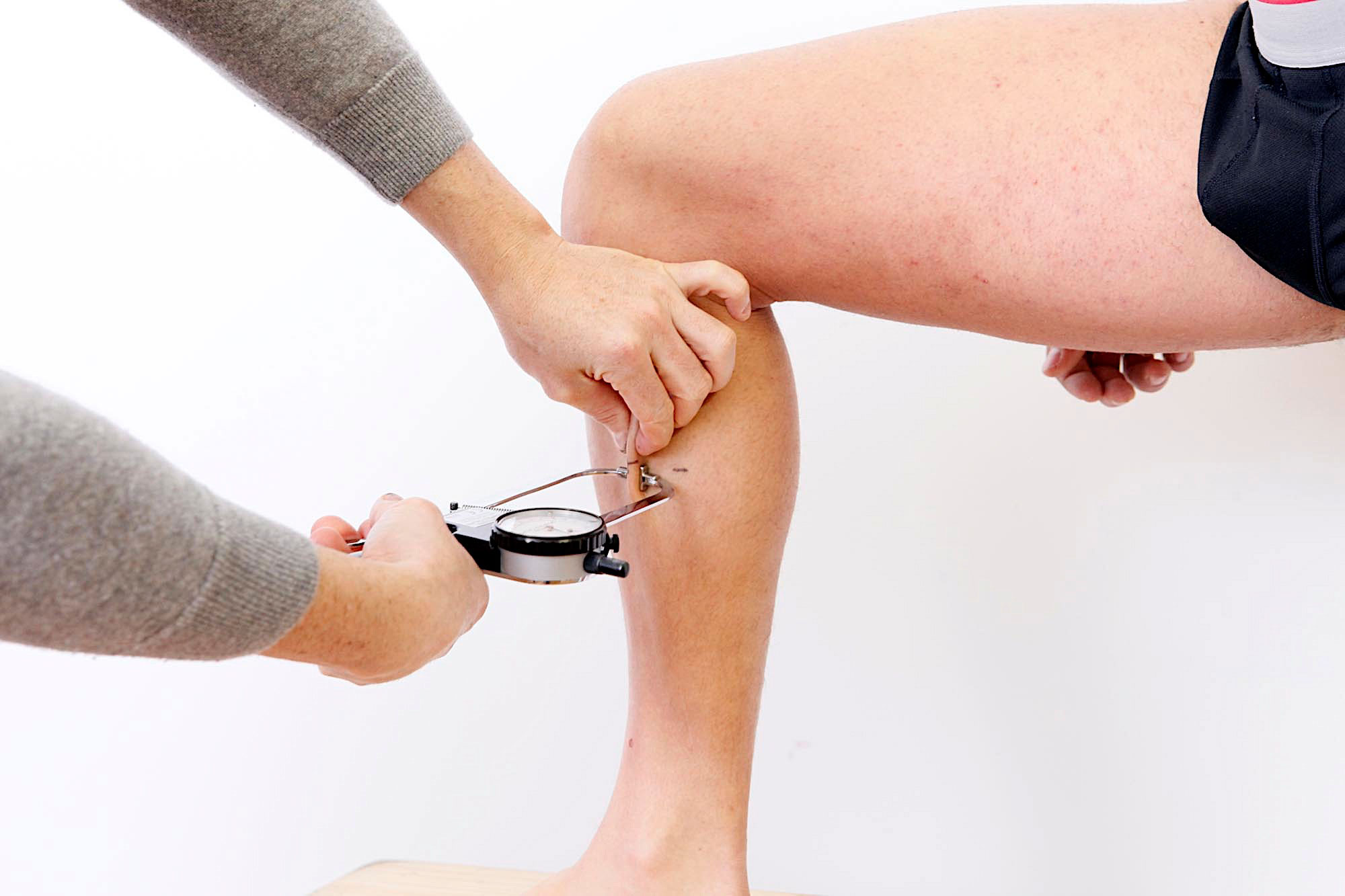
En lo referente a los pliegues, se midieron los mismos con un calibre Harpenden en los cadáveres de 13 mujeres y 12 hombres de entre 55 y 91 años, todos ancianos belgas muertos por causas que no afectaban la composición corporal, como lo puede hacer una patología catabólica que genera una perdida importante de masa muscular. Luego se introdujeron clavos en los sitios de los pliegues hasta hacer contacto con la fascia muscular, y se tomaron fotos de rayos-X para estimar su espesor y compararlo con los pliegues. También se practicaron incisiones en los mencionados sitios par medir otra vez el espesor, y por ultimo se midió el espesor de la piel en cada sitio de pliegue. Al dividir el pliegue medido con el calibre Harpenden por el espesor del mismo medido con lo rayos-X y al expresarlo en porcentje, se obtuvo un coeficiente de compresibilidad:

Compresibilidad de pliegue = 100 x (profundidad de incisión – ½ lectura del calibre)/ profundidad de incisión

Tabla de compresibilidad de pliegues del ECB:

El principal problema de los pliegues es la compresibilidad.

Espesor de la piel (mm)

Una vez concluida la disección total, se estudio la correlación entre los pliegues y la masa adiposa total. Se descubrió que dos sujetos con una cantidad de tejido adiposo similar podían tener pliegues muy diferentes, como lo indica el diagrama:

La distribución de adiposidad sobre el cuerpo tampoco fue muy constante. Por ejemplo:

Distribución de tejido adiposo (%) en cadáveres

Otro problema es la relación entre el tejido adiposo visceral (TAV) y la adiposidad subcutánea, ya que los pliegues no pueden medir este tejido, excepto con la ayuda de un Harakiri. Martin y sus colegas en este estudio no encontraron correlaciones significativas entre los pliegues subcutáneos y el TAV, aunque si con el tejido adiposo total. Esto es de esperarse ya que el TAV no suele ser un gran componente del tejido adiposo total.

Por supuesto tengamos en cuenta que esta distribución de adiposidad corporal es típica en adultos mayores, donde la disminución de estradiol en mujeres les constituye un patrón de distribución más similar al masculino.

Estos excelentes estudios demuestran la falta de robustez de los métodos para estimar la masa adiposa a partir de los pliegues cutáneos, llevando a Alan Martin a concluir con su visión personal de que no tiene sentido agregar mas error biológico a la estimación del tejido adiposo utilizando pliegues cutáneos. ¿Será tan así? ¿Y entonces que alternativas nos quedan? Faltan respuestas prácticas para estos problemas.

Finalmente, las suposiciones de constancia biológica para que la estimación de adiposidad por medio de los pliegues resulte son:

• que la compresibilidad es constante
• que el espesor de la piel es insignificante o constante para todos los pliegues
• que la distribución de la adiposidad es uniforme en el cuerpo
• que la fracción lipidica del tejido adiposo sea constante
• que la proporción entre adiposidad visceral y subcutánea sea fija.

Validación del modelo de dos componentes químicos:

Tal vez el objetivo principal del ECB fue el de poner a prueba los modelos para estimar la composición corporal. Si bien no se midió directamente la grasa o lípidos químicamente definidos (extraíbles por alcohol éter), se midió la masa adiposa. Por medio de estudios posteriores (Martin y colegas 1994) se estimo la fracción lipidica del tejido adiposo en seis cadáveres masculinos no-embalsamados con 9,7 a 25,7 kg de tejido adiposo, variando esta entre un 54 y 85%. La fracción de agua de este tejido también vario desde un 14 a 34%, disminuyendo a medida que aumentaba la cantidad de adiposidad en el sujeto. O sea que cuando más gordo es un sujeto, mayor fracción lipidica contiene su tejido adiposo, cuya ecuación de regresión predicativa:

Fracción lipidica = 0,327 + 0,0124 (% adiposidad)

Por ejemplo, comparemos dos personas con adiposidades del 28,1% (el menor % hallado en los 25 cadáver) y 40,5% (el mayor % hallado en los 25 cadáveres):

(1) Fracción lipidica = 0,327 + 0,0124 (28,1) = 67,5% x 18,5 kg tejido adiposo = 12,5 kg grasa

(2) Fracción lipidica = 0,327 + 0,0124 (40,5) = 82,9% x 25,8 kg tejido adiposo = 21,4 kg grasa

O sea que la persona con mayor cantidad de tejido adiposo posee un 39,5% más de tejido adiposo pero un 71,2% mas de reserva de lípidos, o unas 80,100 kcalorias extras. Tal vez es una estrategia evolutiva para facilitar el transporte de quienes tienen mas tejido adiposo.

En resumen, todos estos hallazgos desacreditan las suposiciones de constancia biológica aplicables a la utilización de pliegues cutáneos para estimar la adiposidad corporal. Seguramente un estudio mas profundo de la variabilidad de los pliegues con herramientas de diagnostico por imágenes como ultrasonido o resonancia magnética podrán generar coeficientes de ajuste para incrementar la validez de los pliegues, así como también el estudio del patrón de compresibilidad en determinados sitios, personas y edades.

Ahora el objetivo era validar las suposiciones de constancia biológica aplicables al modelo químico de hidrodensitometria. Recordemos que el gran problema no era hallar la densidad corporal con precisión y exactitud, sino la conversión de densidad corporal en porcentaje de grasa. Este es el eje de la cuestión, y necesitábamos que la masa magra o libre de grasa sea constante en cuanto a sus proporciones y densidades. Veamos los resultados de composición corporal del ECB, fraccionada en los cinco componentes anatómicamente definidos y diseccionables, piel, adiposo, músculo, óseo y residual (vísceras y órganos):

Observamos de esta tabla que el desvío estándar de los componentes de la masa libre de tejido adiposo (MLTA – un análogo a la MLDG) son bastantes elevados, sobre todo en cuanto a las masa muscular. Recordemos que estos sujetos no representan la variabilidad poblacional mundial en cuanto a edades, razas y tipos de actividades físicas, son apenas una pequeña muestra de ancianos belgas de raza blanca, por lo que si en este estrecho grupo encontramos tanta variabilidad en los tejidos, ¡imagínense en la población mundial! Haciendo un análisis mas detallado de los componentes de la MLTA obtenemos:

Bien, vemos que el rango de variación para la MLTA no es constante, sino la siguiente:

            Piel:                  6,1 a 11,4 % (5,3 %)

            Músculo:           41,9 a 59,4 % (17,5 %)

            Óseo:                16,3 a 25,7 % (9,4 %)

            Residual:          16,3 a 24,6 % (8,3 %)

En cuanto a las densidades del tejido óseo (el único tejido cuya densidad varía significativamente) se encontraron los siguientes valores para los 25 cadáveres:

Queda poco para poder defender el modelo químico bi-compartamental. Lamentablemente las sospechas se hicieron realidad y el método quedo invalidado con esta publicación en 1984. El efecto del ECB sobre la comunidad científica fue extraño: mientras unos investigadores se apresuraban a generar nuevos modelos con los datos antropométricos validados contra los tejidos de los cadáveres, otros decidieron usar simplemente la suma de 5, 6 o 7 pliegues como indicador absoluto de adiposidad (casos de Australia y Canadá), y el “establishment” norteamericano de la composición corporal se sintió ofendido y no adopto (hasta la fecha de hoy) estos avances, optando por continuar con la misma corriente que les había generado notoriedad, publicaciones, fondos para investigación y carreras como docentes universitarios. Hoy en día, unos 20 años después del ECB, siguen apareciendo libros y tratados sobre la composición corporal que ignoran parcial o completamente la existencia e implicancias del ECB. El ECB ha sido el estudio más importante de la historia de la composición corporal, sin duda, e ignorarlo o rechazarlo sobre el argumento de que “solo eran ancianos belgas” es no comprender o no querer comprender la importancia del mismo.

¿De que manera se podría utilizar el sistema químico de dos componentes en medicina deportiva? Puede ser de utilidad como un modelo que a pesar de no ser valido puede clasificar a sujetos y diferenciarlos entre ellos con fines de salud y deporte. Pero para que esto sea una decisión inteligente hay que utilizar una ecuación especifica en poblaciones de sujetos muy similares entre si. Por ejemplo utilizar la ecuación de Parizkova y Buzkova (1971) en deportistas masculinos adultos, como hacen en Cuba. En este caso no es tan importante si la grasa esta sub- o sobre-estimada, sino que la ecuación me permita averiguar el estado actual del deportista, comparándolo con valores de referencia establecidos con la misma ecuación, y luego ir monitoreando los cambios debidos a las cargas de entrenamiento o intervención nutricional.

Músculo:

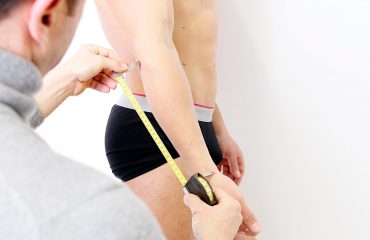
Procesando datos de 12 cadáveres masculinos, Alan Martin (1990) publica una ecuación de regresión para la estimación de la masa muscular. Comienza el artículo manifestando su sorpresa por la ausencia relativa de tales ecuaciones, con un énfasis excesivo en la estimación de la grasa corporal. Su aplicación, continua, abarca varias áreas además de la medicina deportiva: evaluación y control de estados de desnutrición y anorexia, dosificación farmacológica, estudio de los efectos de la inmovilización, monitoreo de la atrofia, y como indicador de maduración biológica. La estrategia del modelo fue de utilizar la suma de perímetros corregido por pliegues, multiplicado por la estatura y una constante de cálculo. La elección de sitios a utilizar corresponde a aquellos que tuvieron una mayor correlación con la masa muscular total en esta muestra de cadáveres, donde curiosamente el perímetro corregido del brazo, largamente utilizado como indicador de las reservas proteicas, no mejoro la predicción y no fue incluido en la ecuación final.

La masa muscular suele disminuir con la edad excepto para Iggy Pop de mas de 50 años.

Masa muscular (g) = talla (cm) * (0,0553*CTG² + 0,0987*FG² + 0,0331*CCG²) – 2445 (Martin y cols, 1990)

CTG = perímetro de muslo medio corregido por pliegue homónimo

FG = perímetro de antebrazo máximo sin corregir por pliegue

CCG = perímetro de pantorrilla máximo corregido por pliegue homónimo

Para obtener el perímetro corregido la estrategia es la siguiente:

Perímetro corregido = Perímetro del miembro (en cm) – [pliegue del miembro (¡pasado a cm!)*pi (o sea: 3,141)]

 El coeficiente de determinación (R²) de esta ecuación fue de 0,97 (o sea, excelente para predecir la masa de los cadáveres) y el error de estimación estándar (EEE) 1,53 kg (también muy bueno). Pero como es una ecuación de regresión múltiple tiene la particularidad de ser muy representativa de la muestra, que en este caso eran ancianos belgas masculinos. No debería utilizarse esta ecuación en otros grupos, a pesar de que esto ha ocurrido en investigaciones sobre deportistas jóvenes varones e incluso en nadadoras femeninas en el estudio KASP (Kinanthropometry Aquatic Sports Project, 1994). Esto fue aclarado por los autores, pero su uso se debió a la ausencia de alternativas mejores. Martin no diseño una ecuación similar para mujeres porque la muestra del ECB eran ancianas con un 42 % de masa adiposa y mucha variabilidad en la compresibilidad de los pliegues. Al año siguiente de su publicación, el mismo autor junto a su colega Linda Spenst publica valores de masa muscular en diferentes grupos de atletas de elite y los compara con hombres no-deportistas para tener un referente. Expresan los resultados en términos absolutos y relativos al peso corporal:

En baloncesto existe mucha masa muscular debido a la gran estatura.Como podemos observar de estos datos, la ecuación nos permite clasificar y comparar la masa muscular de diferentes grupos, siendo los físico-culturistas los más musculazos en términos absolutos y relativos, y es interesante observar el efecto de la estatura. Los jugadores de baloncesto poseen 54,7 kg de masa muscular, mientras que los corredores de 400 metros solo 40,4 kg, pero estos últimos tienen un porcentaje relativo de músculo mayor que los anteriores (61,7 contra 60,9 %) debido a poseer menores valores de grasa (expresado como la suma de 9 pliegues). Otro hecho interesante es el incremento de masa muscular a medida que aumenta la intensidad de la prueba de pedestrismo, y que los fondistas tenían menor masa muscular absoluta que los no-deportistas.

En 1997 un canadiense de nombre Doupe modifica la ecuación de Martin para utilizar otras variables antropométricas para estimar la masa muscular. Este investigador se toma el trabajo de hacer esto porque quiere calcular la masa muscular de los 23,400 canadienses que fueron medidos en el Canada Fitness Survey de 1981, donde no se midió ni el perímetro de muslo medio ni el de antebrazo que requieren la ecuación de Martin, pero si los perímetros de muslo máximo y brazo relajado. Doupe estaba interesado en ver el efecto del envejecimiento sobre la masa muscular, y sus aplicaciones a la movilidad, terapias nutricionales y farmacológicas, y tratamiento de patologías. También demostró que el fumar incrementaba la perdida de masa muscular.

Masa muscular (g) = talla (cm) * (0,031*MUThG² + 0,064*CCG² + 0,089*CAG²) – 3,006 (Doupe y cols, 1997)

MUThG = perímetro de muslo máximo corregido por pliegue supra-espinal (¡si, el supra-espinal!)

CCG = perímetro de pantorrilla máximo corregido por pliegue homónimo

CAG = perímetro de brazo relajado corregido por pliegue de tríceps

El coeficiente de determinación (R²) de esta ecuación fue de 0,96 (o sea, excelente para predecir la masa de los cadáveres) y el error de estimación estándar (EEE) 1,488 kg (también muy bueno).

En el año 2000 Lee y colegas del grupo de Steven Heymsfield del St. Luke’s-Roosevelt Hospital de Nueva York generaron otra ecuación de regresión múltiple para estimar la masa muscular con antropometría simple. El concepto fue similar a las anteriores aquí mencionadas, que supone que las ¾ partes de la masa muscular se encuentra en los miembros, y que la mayoría de la composición de los miembros es músculo. Por eso eligen perímetros de los brazos y piernas, pero no del tronco. La gran diferencia de este estudio radica en que en vez de cadáveres para validar la ecuación utilizaron imágenes obtenidas por resonancia magnética nuclear (RMN) en sujetos vivos (n = 244) que incluían un rango de edades, sexo y razas.

Cortes seriados de muslos para estudiar su composición.Como vemos, la muestra es relativamente grande, e incluye ambos sexos y cuatro grupos raciales. En la ecuación se incluyen coeficientes diferentes según estos aspectos, permitiendo al modelo aplicaciones a una proporción mayor de la población. Los criterios de exclusión eran tener menos de 20 años de edad, padecer alguna patología, estar tomando fármacos que afecten el peso y la composición corporal y también estar participando de un programa estructurado de actividad física. Este último factor es importante para la aplicación en deportes: se excluyen atletas de la muestra, tal vez generando ecuaciones que sobre-estimen la masa muscular en deportistas al igual que la de Martin. La masa muscular fue estimada a partir de unos 41cortes o tajadas de imágenes desde pies a manos extendidas atrás de la cabeza con un resonador 1,5 Tesla (General Electric). Cada medición de este tipo tardaba unos 25 minutos y los datos transversales se analizaron con un software especial para calcular el volumen de la masa muscular y luego el peso.

Las medidas antropométricas utilizaron los protocolos de estandarización de la convención de Arlie, Virginia (1988) publicados por Lohman y Roche. Si bien el protocolo no es el de la ISAK, los sitios de medición son casi iguales. Recordemos que tanto en esta ecuación como en la de Martin el perímetro de muslo medio se tomo sobre el punto medio establecido como la distancia media entre el pliegue inguinal y la parte superior de la rotula, y no como el punto medio entre el trocánter y el tibial-lateral. Esto es importante ya que este protocolo de medición arroja valores algo menores al encontrarse el punto medio unos centímetros mas abajo. Los datos se relevaron en dos centros, y en uno se utilizo un calibre Harpenden y en el otro un Lange. Sabemos que existen diferencias entre ambos, con el Lange aportando una tensión mucho menor y pliegues de valor mayor. Esta podría ser una crítica a este estudio que de otra manera es brillante. Es interesante añadir que este grupo de investigación que durante años se dedico a la investigación de la composición corporal por medios químicos cada vez mas complejos finalmente se dedica a la estimación de tejidos anatómicos creando ecuaciones para ser utilizadas con antropometría de bajo costo. Es un golpe de timón en la dirección correcta según mi opinión.

Localización del punto de muslo medio.

Masa Muscular (kg) = Talla (cm)*(0,00744*CAG² + 0,00088*CTG² + 0,00441*CCG²) + 2,4*sexo – 0,048*edad + raza + 7,8 (Lee y cols, 2000)

Sexo = 0 femenino; 1 masculino

Raza = -2,0 asiáticos; 1,1 afro-americanos; 0,0 para hispanos y blancos

CAG = perímetro de brazo relajado corregido por pliegue de tríceps

CTG = perímetro de muslo medio corregido por pliegue de muslo frontal

CCG = perímetro de pantorrilla máximo corregido por pliegue homónimo

El coeficiente de determinación (R²) de esta ecuación fue de 0,91(excelente) y el error de estimación estándar (EEE) 2,2 kg (también muy bueno).

Resonancia magnética nuclear para estudiar composición corporal.

Consideraciones finales:

He incluido aquí las tres ecuaciones de masa muscular mas recientes y con buena validación ya sea en cadáveres o con diagnostico por imágenes (tal vez el nuevo Gold Standard). Existen otras teniendo en cuenta la excreción urinaria de creatinina, o solo utilizando los datos del brazo, que han demostrado poseer mucho error. No he abarcado en esta sección las ecuaciones correspondientes a técnicas de fraccionamiento anatómico como las de Matiegka, Drinkwater y Ross, De Rose y Guimaraes, y Kerr y Ross. Estas serán estudiadas mas adelante en la sección sobre fraccionamientos.

Hueso:

Utilizando un procedimiento de correlación y análisis de regresión múltiple similar al de la masa muscular y también basándose en el trabajo original de Matiegka de 70 años antes, Martin (1991) publica la siguiente ecuación para la estimación de la masa ósea a partir de la antropometría:

Masa Esquelética (kg) = 0,60 * 0,0001 * Talla (cm) * (Suma de diámetros óseos)² (Martin, 1991)

Suma de diámetros óseos = humeral + femoral + muñeca + tobillo

Esta ecuación mejoro las anteriores de von Doblen (1964) y Alexander (1964) que tendían a sobre-estimar la masa esquelética, al menos al aplicarla a los resultados de los cadáveres de Bruselas. El promedio de masa esquelética en estos cadáveres fue de 9,3 kg (desvío estándar 1,4 kg) para hombres, 7,7 (d e 1,3 kg) para mujeres y un rango de 6,7 a 11,7 kg.

Para la formulación de la misma ecuación, Martin eligió los diámetros que mayor correlación tuvieran con la masa total del esqueleto, sorprendiéndose al encontrar que los de muñeca y humero fueran mayores predictores que el femoral o el bi-acromial. Observemos en la siguiente tabla los coeficientes de correlación entre variables óseas y la masa esquelética en cadáveres:

Las suposiciones de constancia biológica para que esta ecuación funcione son:El diámetro de muñeca estima la masa esquelética.

1. la antropometría mide de manera exacta las dimensiones óseas
2. la forma de un hueso particular no cambia entre las personas
3. la densidad ósea es constante
4. la masa de los huesos seleccionados es una proporción constante con la masa total del esqueleto

Una vez mas, nos encontramos con la limitación de que la antropometría no puede medir la densidad mineral ósea, eso solo se realiza con maquinas especializadas como la densitometría dual por rayos-X (DEXA). Falta estudiar más las asociaciones entre variables antropométricas y densidad mineral ósea para poder utilizar la antropometría para estimarla, aunque es probable que los resultados no sean muy alentadores debido a la gran sensibilidad metrologica necesaria para estimar la DMO.

Índice músculo/óseo:

La estimación antropométrica de la masa esquelética sirve por en cuanto para aplicarla en grupos homogéneos de personas sin patologías ni osteoporosis. Una utilización común en deportes es utilizar el índice músculo/óseo como un cociente indicador de rendimiento biomecánico, una suerte de “índice motor/chasis” aplicable a humanos. En teoría, cuanto mayor es la proporción de masa muscular en relación a la ósea, con mayor potencia se podrá trasladar el cuerpo en el espacio. Para esto consideramos que el esqueleto corresponde a “peso muerto” y que la masa muscular es la “masa activa” que genera movimiento. No se toma en consideración para este índice la masa adiposa, que es otro gran “peso muerto” que hay que trasladar y que puede ciertamente disminuir la potencia. En este ultimo caso podríamos calcular un índice músculo/resto del cuerpo.

Estudios en deportistas de elite: KASP y SOKIP

Índice músculo/óseo = Masa muscular (kg)/ Masa ósea (kg)

Este índice se ha utilizado en dos publicaciones referentes a estudios sobre deportistas de elite: los proyectos KASP (mundial de natación en Australia, 1990) y SOKIP (campeonato sudamericano de balompié en Uruguay, 1995). Los resultados fueron sobre las ecuaciones de Martin para ambas masas corporales:

Podemos observar de estos datos como la función en el campo de juego selecciona a jugadores con las características más acorde a la optimización de la función. Es así como los arqueros son los mas robustos y grandes, seguidos por los delanteros y defensores centrales, mientras que los que se desplazan mayor distancia o requieren mayor velocidad (medio-campistas y laterales) suelen tener menor masa corporal, estatura, masa muscular y esquelética. La mayor potencia biomecánica la tendrían los delanteros centrales con un índice de 4,77, y la menor los medio-campistas (los de mayor despliegue aeróbico) con 4,44 y 4,47. Se necesitan estudios que correlacionen este índice con pruebas de campo de potencia, como capacidad de salto o velocidad, ajustando los valores por las diferencias de masa adiposa. Hasta ese momento todo queda en lindas hipótesis.La masa muscular es fundamental en el fútbol.